Vectorización

Última actualización: 2025-05-06 | Mejora esta página

Tiempo estimado: 25 minutos

Hoja de ruta

Preguntas

¿Cómo puedo operar sobre todos los elementos de un vector a la vez?

Objetivos

Entender las operaciones vertorizadas en R.

La mayoría de las funciones en R están vectorizadas, lo que significa que la función operará sobre todos los elementos de un vector sin necesidad de hacer un bucle a través de cada elemento y actuar sobre cada uno de ellos. Esto hace la escritura de código más concisa, fácil de leer y menos propenso a errores.

R

x <- 1:4
x * 2

SALIDA

[1] 2 4 6 8

La multiplicación se aplicó a cada elemento del vector.

También podemos sumar dos vectores juntos:

R

y <- 6:9
x + y

SALIDA

[1]  7  9 11 13

Cada elemento de x fue sumado a su correspondiente elemento de y:

R

x:  1  2  3  4
    +  +  +  +
y:  6  7  8  9
---------------
    7  9 11 13

Desafío 1

Probemos esto en la columna pop del dataset gapminder.

Haz una nueva columna en el data frame gapminder que contiene la población en unidades de millones de personas. Comprueba el principio o el final del data frame para asegurar que funcionó.

Solución al desafío 1

Intenta esto en la columna pop del dataset gapminder.

Haz una nueva columna en el data frame gapminder que contiene población en unidades de millones de personas. Comprueba el principio o el final del data frame para asegurar que funcionó.

R

gapminder$pop_millions <- gapminder$pop / 1e6
head(gapminder)

SALIDA

      country year      pop continent lifeExp gdpPercap pop_millions
1 Afghanistan 1952  8425333      Asia  28.801  779.4453     8.425333
2 Afghanistan 1957  9240934      Asia  30.332  820.8530     9.240934
3 Afghanistan 1962 10267083      Asia  31.997  853.1007    10.267083
4 Afghanistan 1967 11537966      Asia  34.020  836.1971    11.537966
5 Afghanistan 1972 13079460      Asia  36.088  739.9811    13.079460
6 Afghanistan 1977 14880372      Asia  38.438  786.1134    14.880372

Desafío 2

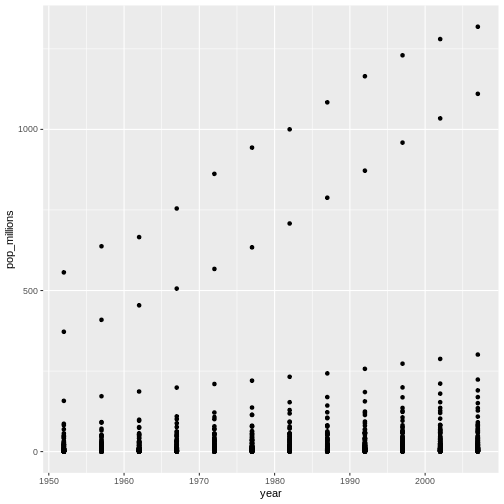
En una sola gráfica, traza la población, en millones, en comparación con el año, para todos los países. No te preocupes en identificar qué país es cuál.

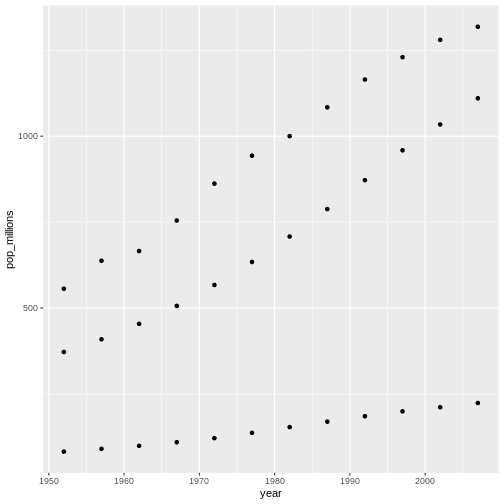
Repite el ejercicio, graficando sólo para China, India, e Indonesia. Nuevamente, no te preocupes acerca de cuál es cuál.

Solución al desafío 2

Recuerda tus habilidades de graficación al crear una gráfica con la población en millones en comparación con el año.

R

ggplot(gapminder, aes(x = year, y = pop_millions)) +
 geom_point()

R

countryset <- c("China","India","Indonesia")
ggplot(gapminder[gapminder$country %in% countryset,],
       aes(x = year, y = pop_millions)) +
  geom_point()

Operadores de comparación, operadores lógicos y muchas otras funciones también están vectorizadas:

Operadores de Comparación

R

x > 2

SALIDA

[1] FALSE FALSE  TRUE  TRUE

Operadores Lógicos

R

a <- x > 3  # o, para más claridad, a <- (x > 3)
a

SALIDA

[1] FALSE FALSE FALSE  TRUE

Sugerencia: algunas funciones útiles para vectores lógicos

any() devuelve TRUE si algún elemento del vector es TRUE all() devuelve TRUE si todos los elementos del vector son TRUE

La mayoría de las funciones también operan elemento por elemento en los vectores:

Funciones

R

x <- 1:4
log(x)

SALIDA

[1] 0.0000000 0.6931472 1.0986123 1.3862944

Operaciones vectorizadas en matrices:

R

m <- matrix(1:12, nrow=3, ncol=4)
m * -1

SALIDA

     [,1] [,2] [,3] [,4]
[1,]   -1   -4   -7  -10
[2,]   -2   -5   -8  -11
[3,]   -3   -6   -9  -12

Sugerencia: multiplicación elemento por elemento vs. multiplicación de matriz

Muy importante: el operador* te da una multiplicación de elemento por elemento! Para hacer multiplicación de matrices, necesitás usar el operador %*%:

R

m %*% matrix(1, nrow=4, ncol=1)

SALIDA

     [,1]
[1,]   22
[2,]   26
[3,]   30

R

matrix(1:4, nrow=1) %*% matrix(1:4, ncol=1)

SALIDA

     [,1]
[1,]   30

Para saber más sobre Álgebra de matrices, ver Quick-R reference guide

Desafío 3

Dada la siguiente matriz:

R

m <- matrix(1:12, nrow=3, ncol=4)
m

SALIDA

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

Escribe lo que crees que sucederá cuando se ejecute:

m ^ -1
m * c(1, 0, -1)
m > c(0, 20)
m * c(1, 0, -1, 2)

¿Obtuviste la salida que esperabas? Si no, pregunta a un ayudante!

Solución al desafío 3

Dada la siguiente matriz:

R

m <- matrix(1:12, nrow=3, ncol=4)
m

SALIDA

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

Escribe lo que piensas que sucederá cuando ejecutes:

m ^ -1

SALIDA

          [,1]      [,2]      [,3]       [,4]
[1,] 1.0000000 0.2500000 0.1428571 0.10000000
[2,] 0.5000000 0.2000000 0.1250000 0.09090909
[3,] 0.3333333 0.1666667 0.1111111 0.08333333

m * c(1, 0, -1)

SALIDA

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    0    0    0    0
[3,]   -3   -6   -9  -12

m > c(0, 20)

SALIDA

      [,1]  [,2]  [,3]  [,4]
[1,]  TRUE FALSE  TRUE FALSE
[2,] FALSE  TRUE FALSE  TRUE
[3,]  TRUE FALSE  TRUE FALSE

Desafío 4

Estamos interesados en encontrar la suma de la siguiente secuencia de fracciones:

R

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

Esto sería tedioso de escribir, e imposible para valores altos de n. Usa vectorización para calcular x cuando n=100. ¿Cuál es la suma cuando n=10.000?

Solución al desafío 4

Estamos interesados en encontrar la suma de la siguiente secuencia de fracciones:

R

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

Esto sería tedioso de escribir, e imposible para valores altos de n. ¿Puedes usar vectorización para calcular x, cuando n=100? ¿Qué tal cuando n=10,000?

R

sum(1/(1:100)^2)

SALIDA

[1] 1.634984

R

sum(1/(1:1e04)^2)

SALIDA

[1] 1.644834

R

n <- 10000
sum(1/(1:n)^2)

SALIDA

[1] 1.644834

Podemos obtener el mismo resultado usando una función:

R

inverse_sum_of_squares <- function(n) {
  sum(1/(1:n)^2)
}
inverse_sum_of_squares(100)

SALIDA

[1] 1.634984

R

inverse_sum_of_squares(10000)

SALIDA

[1] 1.644834

R

n <- 10000
inverse_sum_of_squares(n)

SALIDA

[1] 1.644834

Puntos Clave

Uso de operaciones vectorizadas en lugar de bucles.